Overview
At the Austin Yacht Club, each summer there is a unofficial race each Friday evening called the Beer Can Race. It involves:- Start and Finish same place
- Use bouys at entrance to AYC
- Imaginary line between
- Race around 3 marks in Lake Travis, TX
- The marks are B, E, and K
- In any direction as long as all the marks are rounded.
- The boats start at handicapped times
- Slower boats go first
- Faster boats follow w/ handicap
- The 1st & 2nd Place winners
- Get a bottle of wine!
- Add 30 seconds handicap next race
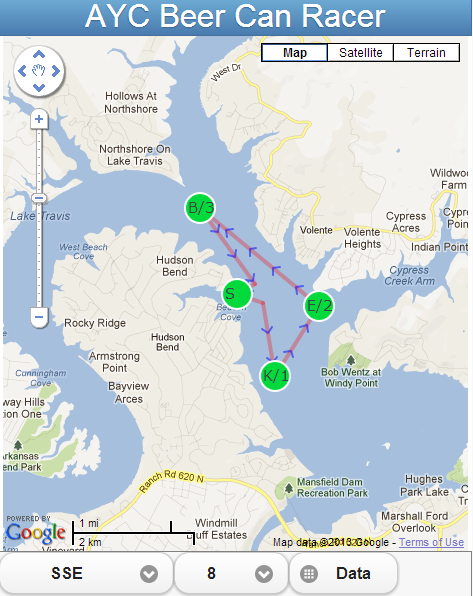
AYC Beer Can Racer
The AYC Beer Can Racer app shown above determines the fastest route around the required marks using the wind direction and speed provided.
Background
This summer I was sailing a beer can race with Ray Shull and as we approached the starting line I wondered which direction he would take. Ray asked me to reach into the cabin and get a chart for him. He looked at the wind direction and then the chart and said "We going to E!". "Wow" I said, "could I have a copy of that chart?" He laughed and said something to the effect that I should figure it out for myself - "it would do you good!"
I had no idea how to pursue this. I wondered what was involved in the calculations. I'd been out of college for more then 30 years and hadn't used much math since. I couldn't remember the difference between a tangent and a cosine.
So I started researching. The first interesting web site was our own AYC. There I found two things that would helped me.
Marks
First, I found the map of AYC Racing Marks http://www.
Next, also from the AYC site, the weather page http://www.
Distance
Now that I had the latitude and longitude of the beer can marks, I needed to know two more things about the marks, the distance between them and the bearing between them all. I found this web site that provided that solution: http://www.movable-
 |
| Distance between two points |
This is where I got lost. I didn't quite understand, given all the information I had, what to do next. Could I use trig and figure the angles the boat would travel and guess at the speed? Should I assume constant speed in all wind directions? Surely I would go different speeds - but how should I guess-estimate that? What should I do about tacking, about land, low water, shifty winds, etc.
Luckily I found something that helped a lot. I found polar data for a Ranger 23 here http://www.arvelgentry.
 |
| Ranger 23 Polars |
Web app
So now I had all the data I needed. I was able to write a very simple web app that works on either Chrome, Safari or Opera desktop browsers. It also works on IPhone because it uses the Safari browser and the Android also. I'm not sure about the other desktop or mobile browsers.
The following is a screen shot from my Android:
Pages
There are three pages for the app.
The first page is a Google map that uses the wind speed/direction from the AYC weather page and plots the fastest route. You can change the speed and direction.
There's also a button on the bottom ("Data") that takes you to a page which is a summary of all the speeds / wind direction and best routes.
 |
| Summary of all Wind Directions and Speed |
There are two buttons on this page, one which is to a line graph for all the wind directions at a specific wind speed. Note that S is the Start/Finish point.
 |
| Chart of all wind directions for specific speed |
The "Map" button returns you to the map.
Calculating the time for each Route
I ignore changing land obstacles due to changes in level of water. I try to guess the route from Start / Finish to / from B & K. As you can see from the map plotting, I show the angles used to clear land obstacles when going in these directions. I assume constant wind. I tack when heading are less then 45 degrees. If the TWA is less then 45, I fall off to 45 and then using trig figure out the two legs of the triangle. Though the Range 23 can sail windward at less then 45 degrees, for my solution, I ignored those angles as the boats I've sailed can't point that high.
All the routes plotted are based on time - what is the fastest route? The fastest route is determined by looking at the possible paths for each route. The time to sail each path is calculated by dividing the distance by the boat speed. The boat speed is obtained from the polar tables using the TWA for the wind direction/speed.
Example calculation
Let's assume we have a SSE wind with 8 knots. There are numerous routes that have to be calculated (KEB, BEK, KBE, BKE, EKB, and EBK).Each of these routes are made up of smaller paths. Let's consider the BEK route. The paths that make up this route are
- S to A (the tack point away from land)
- A to B
- B to E
- E to K
- K to Z (the tack point away from land)
- Z to S (back to the start/finish line)
For demonstration, I'm going to look at three paths of the BEK, namely:
- S to A
- A to B
- B to E
Now "A" and "Z" are pseudo marks that represents a point that extends far enough into the harbor that when rounded avoids the shore line. The sailboat has to extend past this point before tacking to mark B.
S to A
 |
| Polar 105 |
In this case the true wind angle, TWA, is 96. Using the Rangers polar data, we use the polar for the next available TWA which is 105. Looking up the chart, the speed is determined to be 5.665. Since the distance is 0.3373, then the time to travel from S to A is 0.059 (Time = Distance divided by Speed (T = D/S)).
A to B
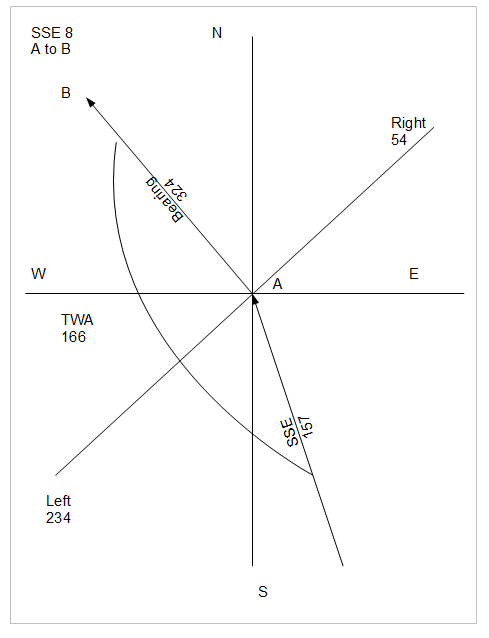 |
| A to B |
In the diagram above, A to B, the wind direction is behind the sailboat and the TWA is 166.
Again, from the above table, the polar twa is 165 and the speed is 3.792. The time to travel from A to B is 0.441.
B to E
This next path shows how the sailboat must tack to make the mark.
 |
| B to E - Step 1 |
In the diagram above, the sailboat takes a new bearing which is a polar TWA of 44 degrees. So what needs to be done now is calculate the length of the New Bearing and the leg from the Tack to mark E.
Using trigonometry, the distance of the New Bearing to the Tack location and the distance from the Tack location to mark E can be calculated.
Note that a Tack makes a 90 degree turn. Therefore we have a right triangle with the hypotenuse being the original Bearing.
Let's call the Bearing "c". Using the Pythagorean theorem,
So what is the length of a, the new bearing? Remembering trig, a = sin(a) * c.
A is the polar of 44 minus 27 which is 17. First though we have to convert degrees to radians and the formula is:
sin(27 * (PI / 180) which gives us 0.276485.
Substituting the values of a and c, using a = sin(a) * c, the distance of the Tack (a) is 0.7047.
Now using Pythagorean, and knowing c & a, we can calculate b:
b = square root (c squared - a squared) = 2.44963.
So now we have our total distance for this New Bearning (b) and Tack (a):
b + a = 0.7047 + 2.44963 = 3.15433
Using the polar data for 44 TWA, see below,
We have the time for this path of B to E:
Time = distance / speed
Time = (a + b) / 4.729;
Time = 3.15433 / 4.729
Time = 0.667
Summary
So continue as above for all the paths that make up BEK route and summing their times, the route takes 1.811 hours to complete.
This process has to be done for all the possible routes and the route with the least amount of time is what is desired.